In this lesson, we will take a look at how to add mixed numbers with fractions. Below are some examples of adding fractions with mixed numbers.
Content:
Before we get into this topic, recall that a proper fraction is a fraction whose numerator is less than its denominator. In addition, a mixed number is the sum of a whole number and a proper fraction, see the image below.

1) Find the sum 41/3 + 1/2:
The key to solve this problem is to remember that a mixed number is the sum of a whole number and a proper fraction. So first, we rewrite the mixed number 41/3 as the sum of the whole number 4 and the proper fraction 1/3.

Let’s focus on the fractions, to add them we can use the butterfly method. In this method, we start by multiplying the denominators (3 × 2) and then we add the cross products (1×2 + 3×1).

Here we have the sum of a whole number (4) and a proper fraction (5/6), so we can rewrite this expression as a mixed number.

The resulting mixed number is 45/6, this number can also be expressed as an improper fraction.
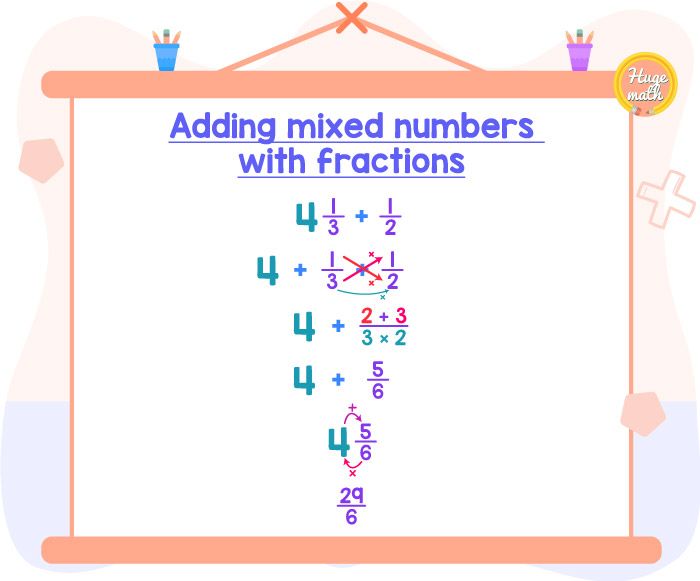
That’s it, the final answer is 45/6 or 29/6.
2) Add 34/5 + 2/3:
First, we rewrite the mixed number (34/5) as the sum of a whole number (3) and a proper fraction (4/5).

Then we can quickly add the 2 fractions (4/5 + 2/3) using the butterfly method.
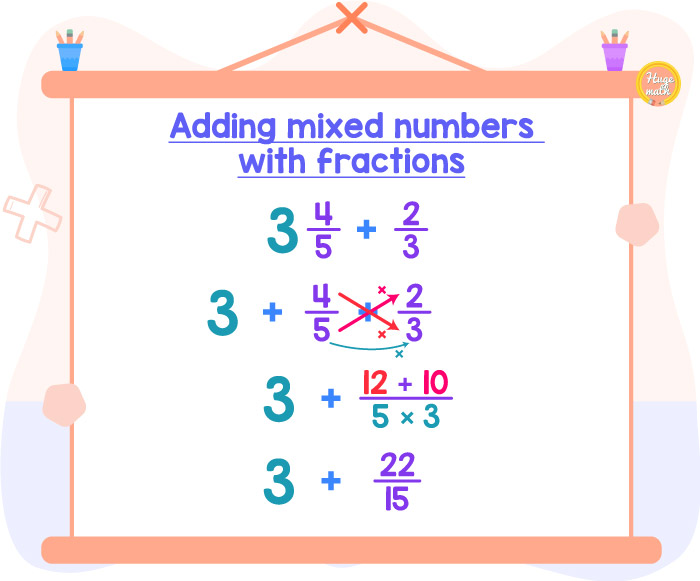
The sum of these 2 fractions is an improper fraction (22/15), and since we don’t want an improper fraction in the final answer, we need to convert it to a mixed number.

Now we have the sum of a whole number and a mixed number, we start by adding the whole numbers together (3 + 1) and then, we write the same fraction (7/15).

The resulting mixed number is 47/15. We can convert this mixed number to an improper fraction.

The answer is 47/15 or 67/15.
Video
In the video below, I will show you more examples of adding mixed numbers with fractions.
References
For this lesson, we have used this book:
- Tussy, K., Gustafson, D. y Koenig, D. (2013). Prealgebra (4th ed.; pp. 374-378). Cengage Learning.