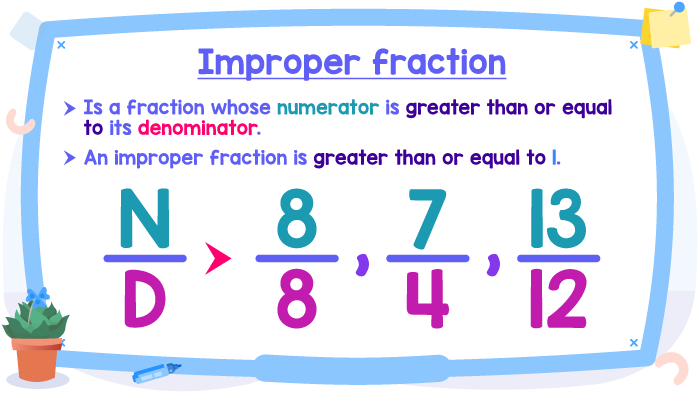
An improper fraction is a fraction whose numerator is greater than or equal to its denominator. Improper fractions are greater than or equal to 1. For example, these are improper fractions because the numerators are greater than or equal to the denominators.
Content:
1) How many blueberry pies are here?
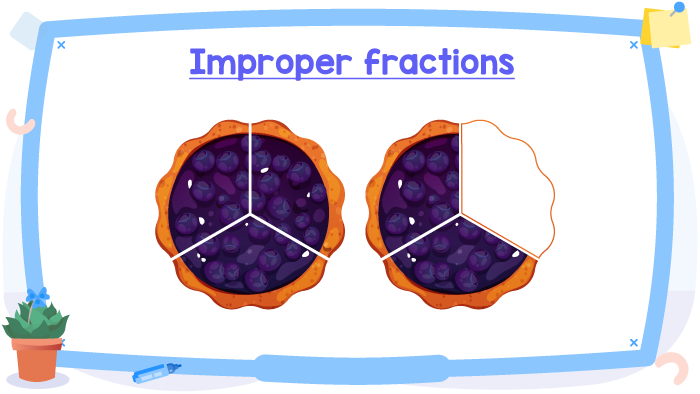
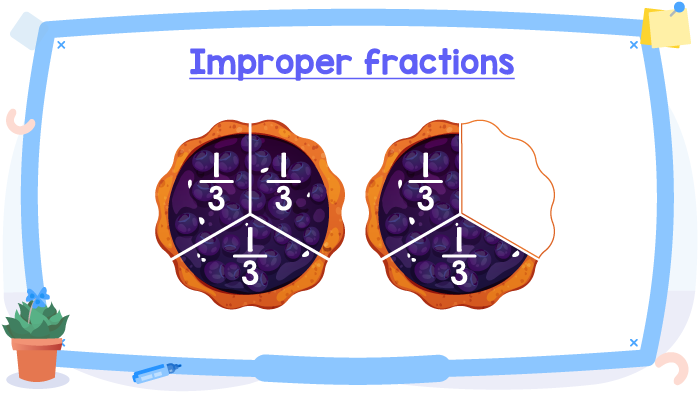
Each pie has been divided into 3 equals parts or 3 equal slices. Thus, each slice represents 1⁄3 of a pie.
In total, we have 5⁄3 pies. Recall that 5⁄3 is an improper fraction, given that numerator (5) is greater than the denominator (3).
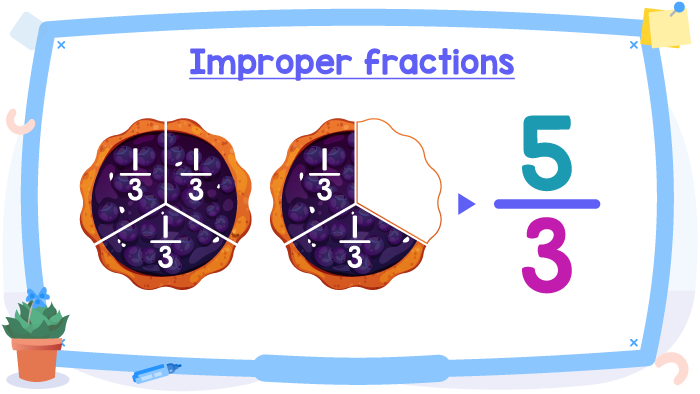
We have taken the first pay completely and we can put together the slices of this pie. We took 1 whole pie and a little of the second pie, I mean, more than 1 whole. Here we can see that our improper fraction is greater than 1, because we have more than 1 whole (pie). This is related to another characteristic of the improper fractions: and improper fraction is greater than or equal to 1.
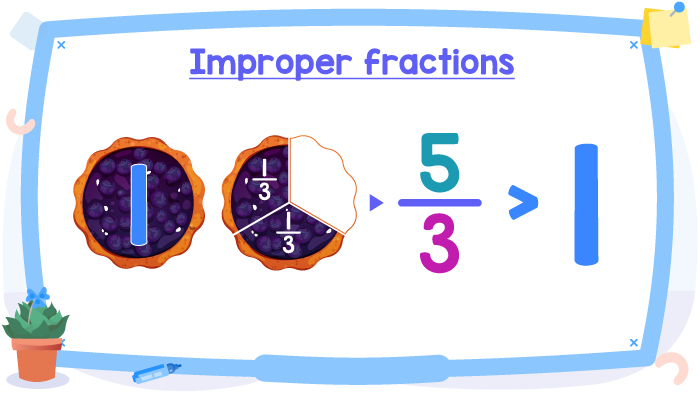
Don’t forget that an improper fraction can be written as a mixed number or a whole number, so, we are going to write our improper fraction 5⁄3 as a mixed number.

This mixed number 12⁄3 is read as “one and two thirds”. Recall that a mixed number contains a whole number and a fraction.
2) How many apple pies are here?
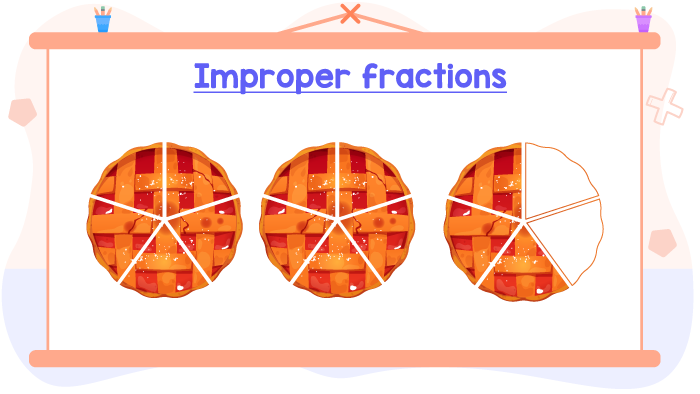
Each apple pie has been divided into 5 equals parts or 5 equal slices. Therefore, each slice represents 1⁄5 of a pie.
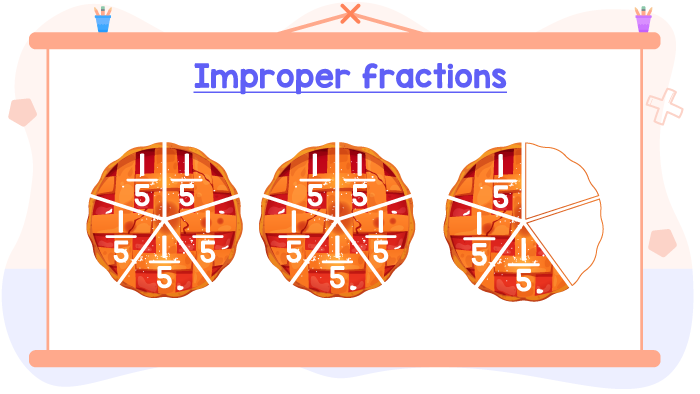
So here we have 13⁄5 pies. Recall that 13⁄5 is an improper fraction, given that numerator (13) is greater than the denominator (5).
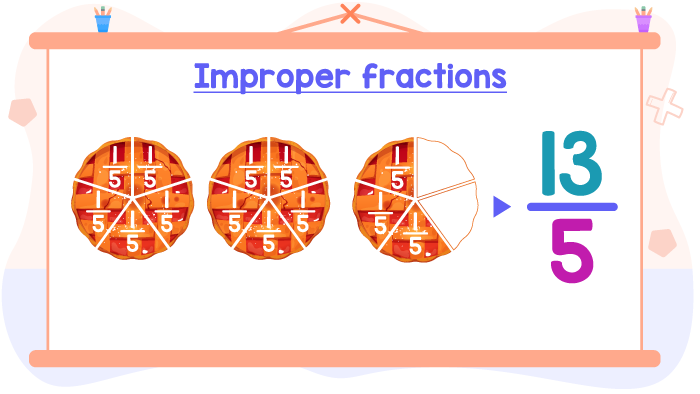
Don’t forget that an improper fraction can be written as a mixed number or a whole number, so finally, we are going to write our improper fraction 13⁄5 as a mixed number. As you can see, we took the first 2 pies completely, so we took 2 whole pies and 3⁄5 of the third pie.

This mixed number, 23⁄5 is read as “two and three fifths”. 2 is the whole number and 3⁄5 is the (proper) fraction.
Exercise:
How many oranges are in the image? Write the answer as an improper fraction and also as a mixed number.

Answer: 11⁄2 or 51⁄2 oranges.
Video
In the following video we will take a look at the improper fractions.
References
For this lesson, we have used these books:
- OpenStax (2020). Prealgebra 2e (pp. 279-285). Rice University.
- Martin-Gay, E. (2020). Basic college mathematics with early integers (4th ed; pp. 179-178). Pearson.
- Aufmann, R. and Lockwood, J. (2014). Basic College Mathematics (10th ed, pp. 70-71). Cengage Learning.
7 thoughts on “Improper fractions (with examples)”